Logistic Regression: A Simple Explanation

Our world is complex and interconnected, and understanding the relationships between various variables is critical for making informed decisions and predicting outcomes. Because there are numerous ways that variables can interact, no single statistical analysis can be applied in every circumstance. As a result, depending on the specific context, a customized approach utilizing appropriate methods must be used. To understand what the appropriate method for our data is, we need to understand the type and the interaction between variables.

There are two primary types of data: numerical and categorical, both of which can be used as dependent or independent variables. The dependent variable is the variable that is observed or measured, whereas the independent variable is the variable that the experimenter controls or manipulates. When we study the relationship between a dependent and independent variable that are both numerical, we can use linear regression (Figure 1a). For example, if we want to know how the amount of time a student spends studying affects their test scores, we can use linear regression to create a line that tells us how much of an increase or decrease in test scores we can expect for each additional hour of studying. When we study the relationship between one categorical independent variable and a numerical dependent variable, we can use the analysis of variance or ANOVA (Figure 1b). For example, if we want to know if average income is “dependent” on education level (high school, college, graduate school), we can use ANOVA to find out if there is a significant difference in income across these categories. In the case we have an independent variable that is numerical and a dependent variable that is categorical we can use logistic regression (Figure 1c). Banks use numerical variables such as income, debt-to-income ratio, and loan amount to classify customers in categorical groups such as “likely to default” or “unlikely to default”. Thus, based on numerical records, the logistic regression can help to determine if bank customers will repay their loans.

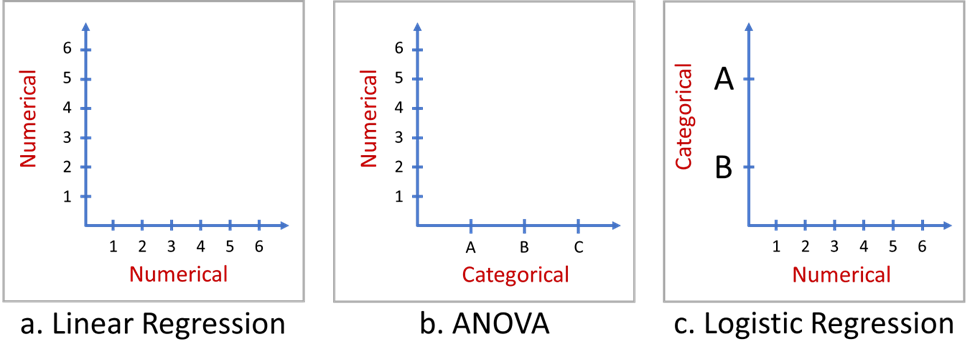
Figure 1. For various types of dependent (y-axis) and independent (x-axis) variables, it is necessary to employ distinct models.

Logistic regression is utilized when the dependent variable is binary, indicating it has two levels only. Logistic regression is a powerful tool for exploring different aspects of animal production; let’s delve into it further. Consider we’re conducting a study within a meat science department to compare the differences between grass-fed and corn-fed beef. Our goal is to use a meat quality variable to determine whether beef comes from grass-fed or grain-fed cattle, which can be useful for meat processing plants’ quality control measures. We can visualize the collected data as in the following figure:

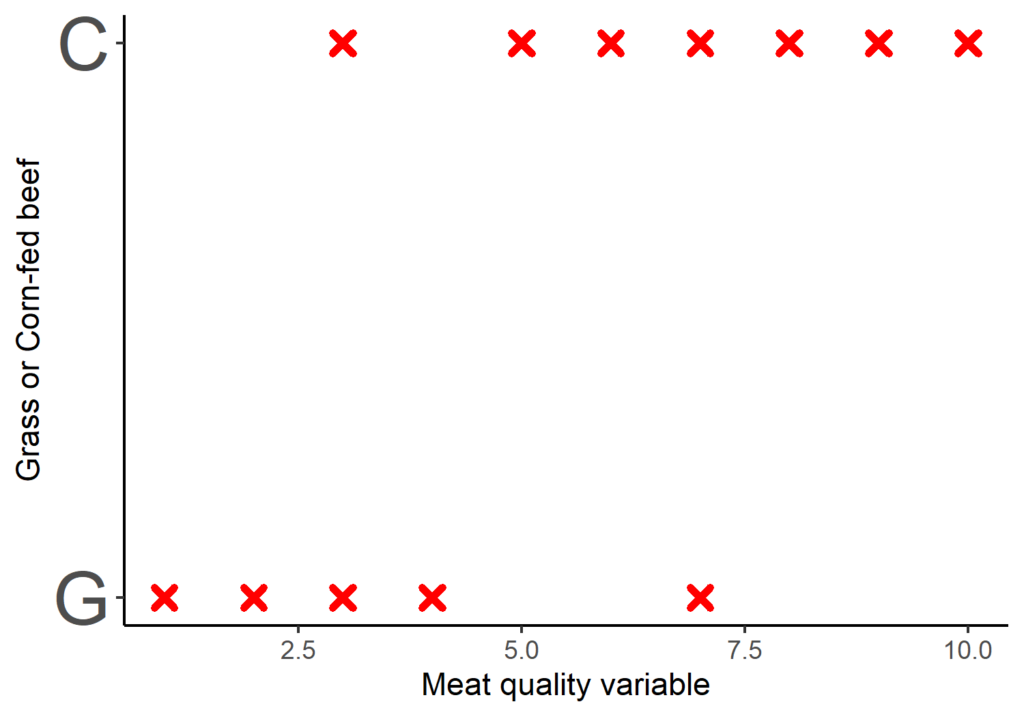
Figure 2. Raw data from our hypothetical experiment.

In the logistic regression approach, the initial stage involves converting the groups into numeric values of either zero or one (Figure 3). The group with the lower numerical value is designated as zero, while the other group is designated as one.

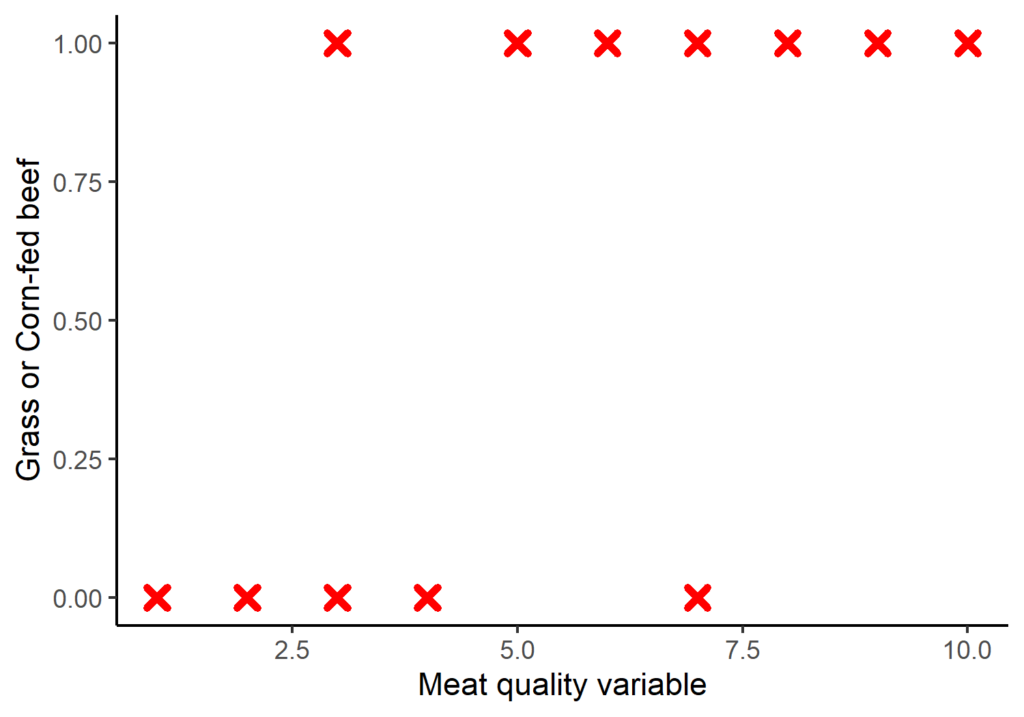
 Figure 3. In the first step of logistic regression, y-axis categories are assigned values of zero or one.

The next step is to fit a logistic function into the data. For that purpose, a method called Maximum Likelihood (ML) is used. The ML method basically place a logistic function and iteratively adjusts its parameters where it fits the best using a likelihood function. The point where the likelihood function is maximized is considered to be optimal.

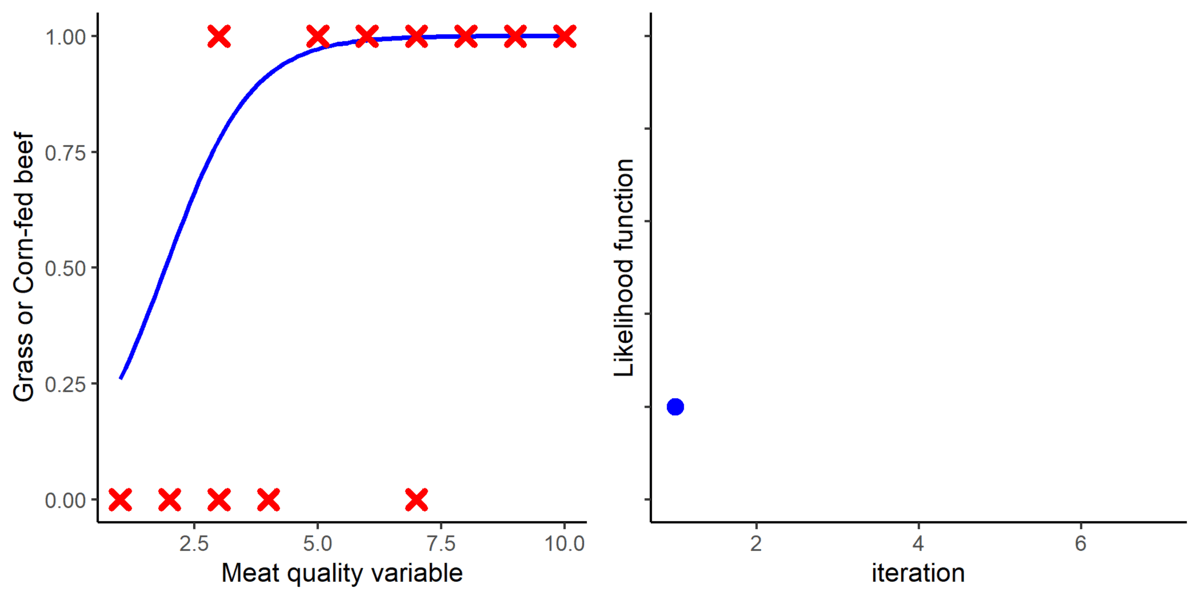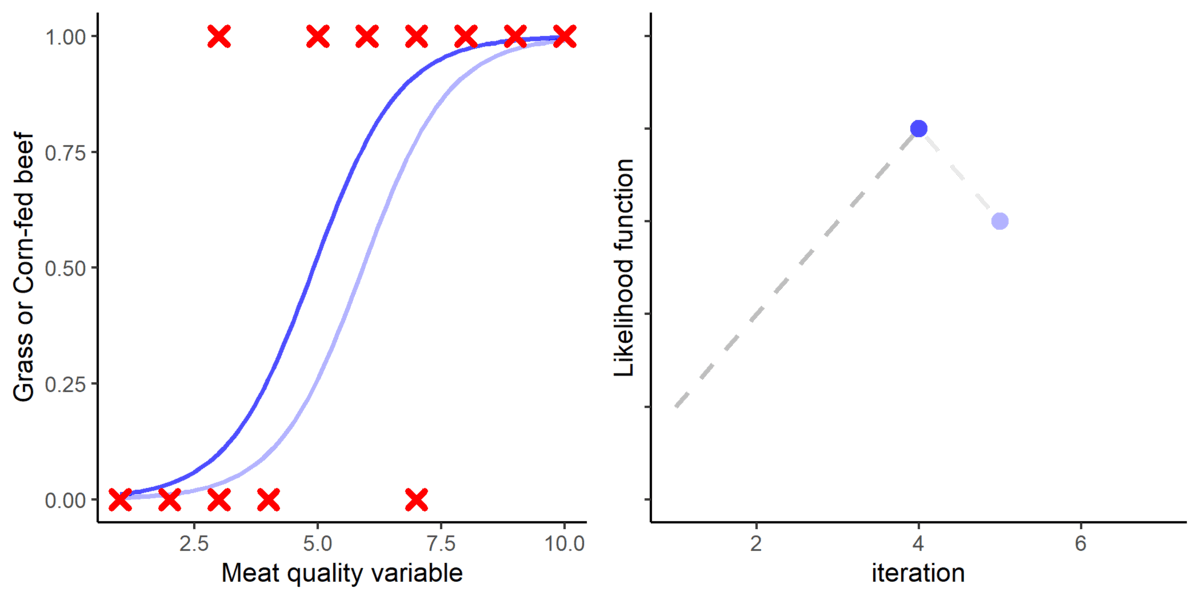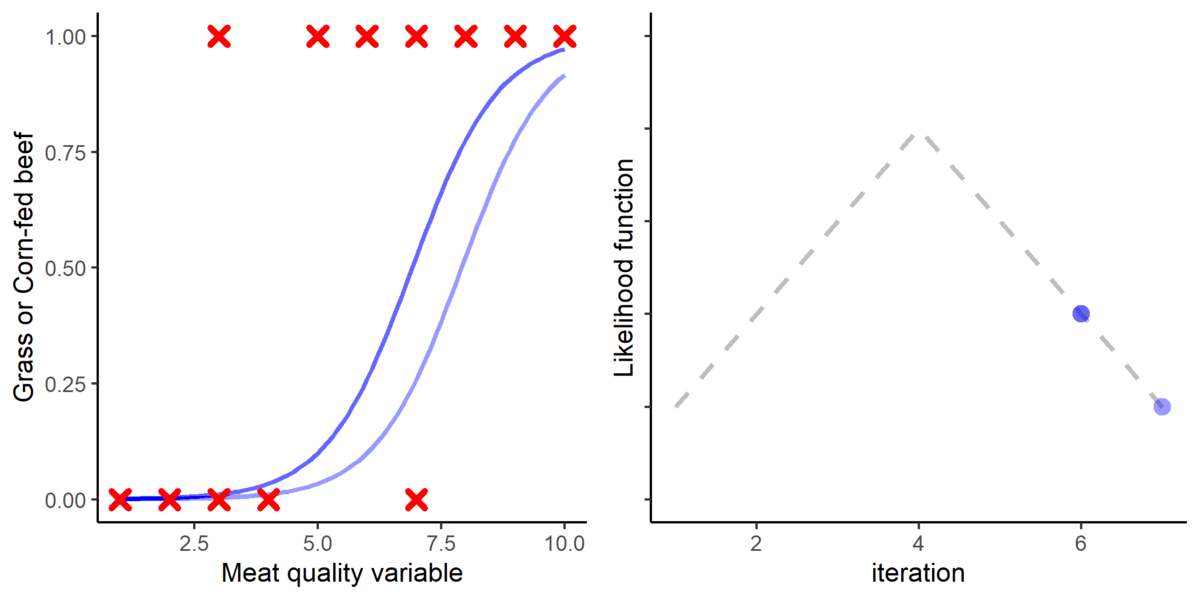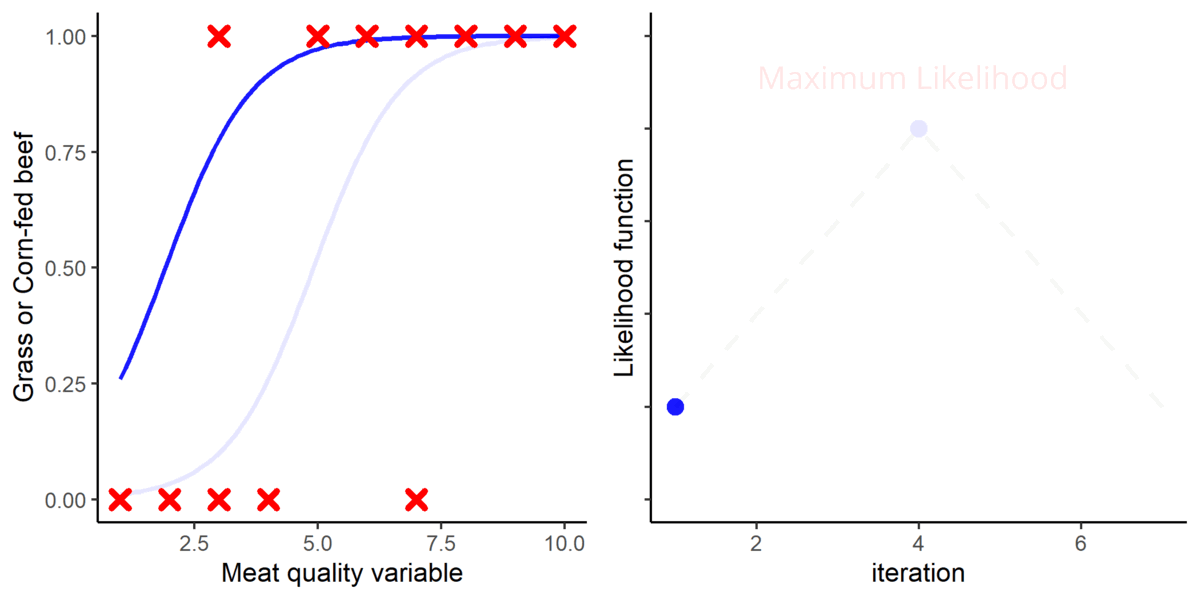
Figure 4. A graphical representation of how the logistic function is fitted using the Maximum Likelihood approach. 

Once the optimal location of the logistic regression is determined, the center of the logistic regression divides the data into two groups. This is known as the cut-off point. Thus, if the x variable is less than the cut-off (in this case 4.95), it is classified as group zero (or Grass-fed beef). If the x variable exceeds the cut-off, it is classified as group one (in this case, Corn-fed beef). Note: The cut-off is not always at center of the logistic regression (or the x value when y=0.5). Sometimes different cut-off values may result in greater classification accuracy. The calculation of the optimal cut-off may be explored in future posts.

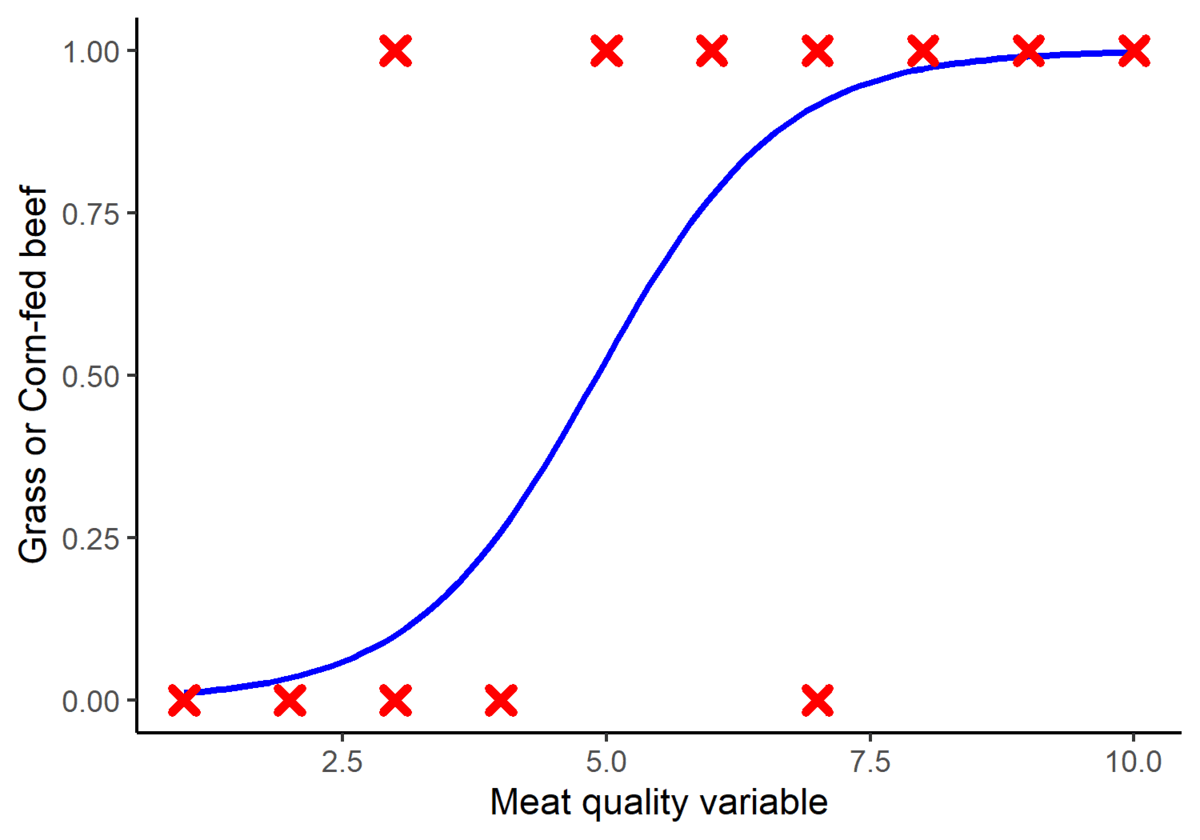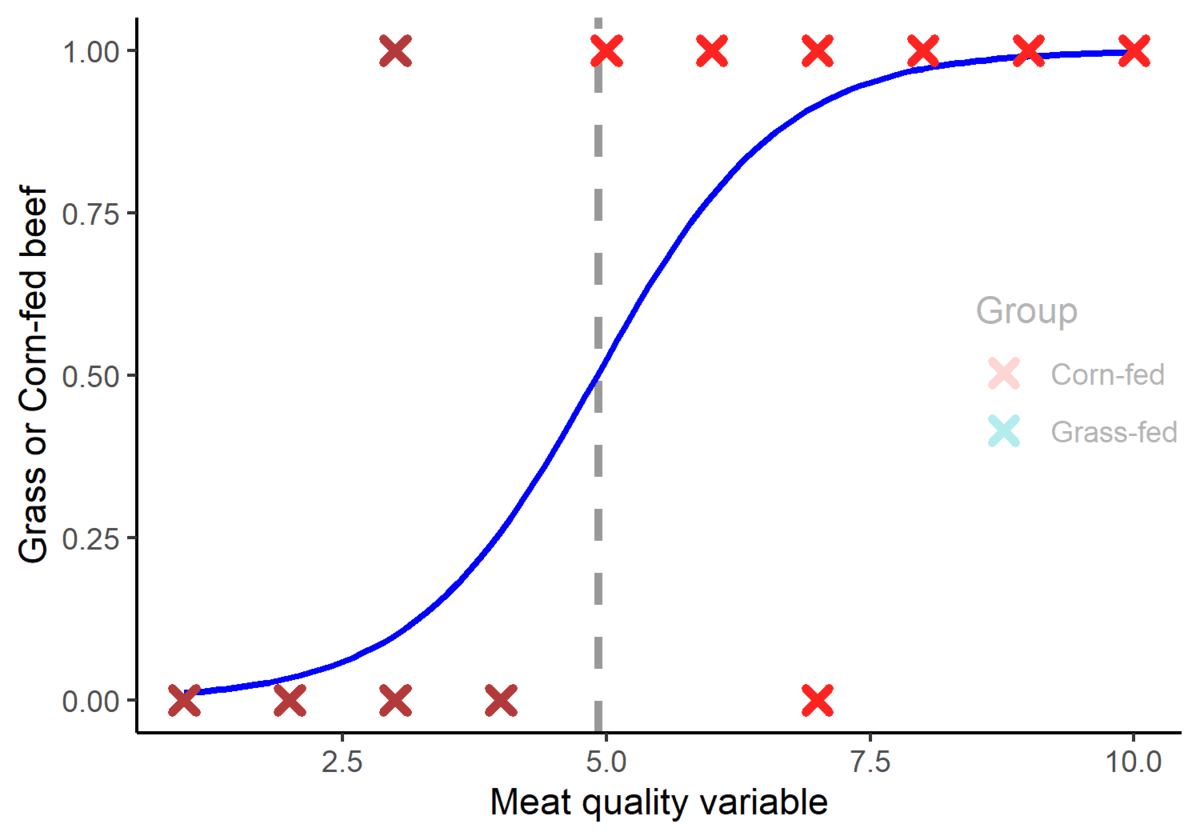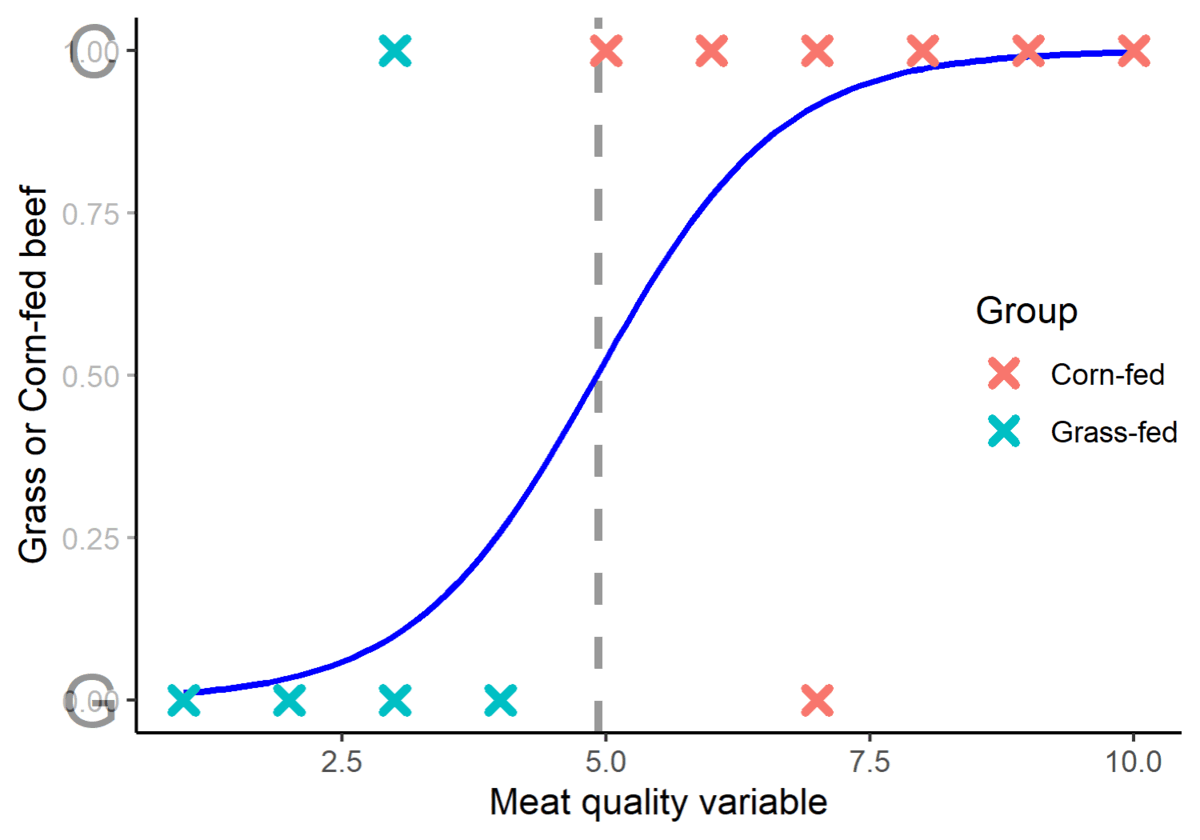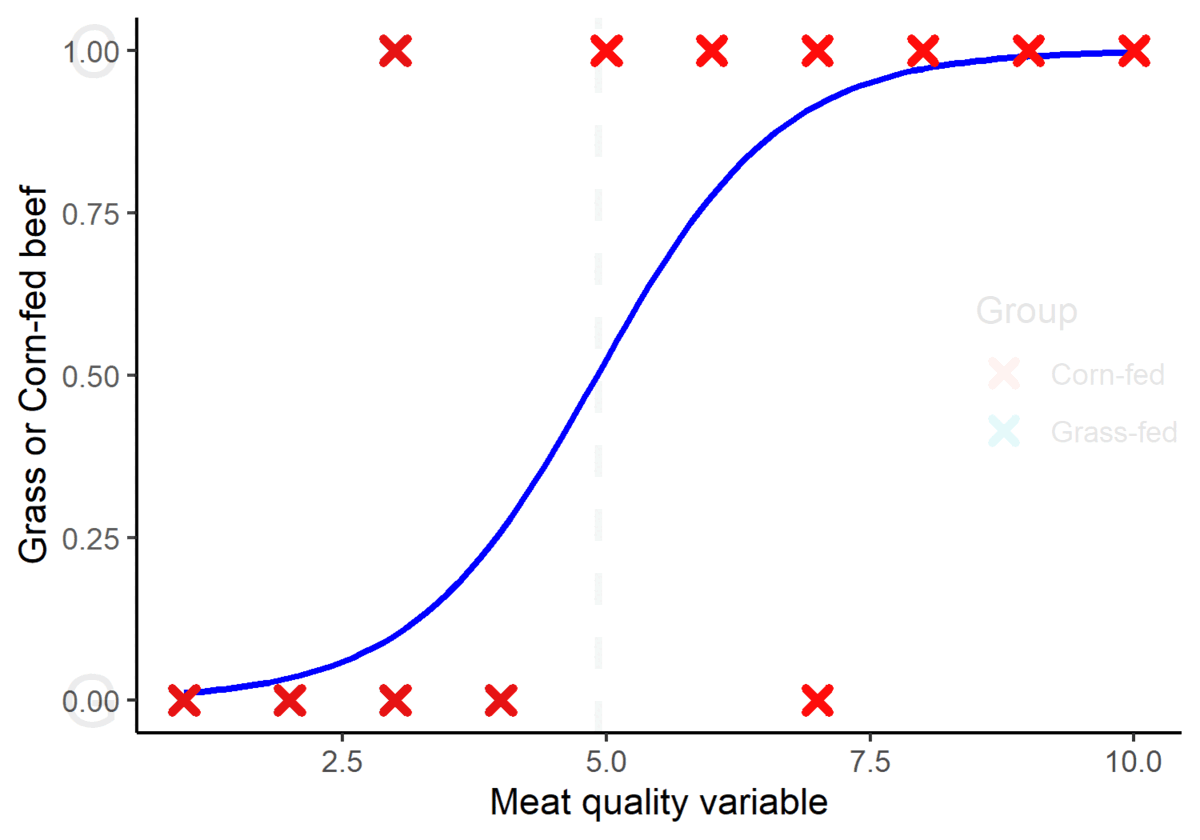
Figure 5. A graphical representation of how the logistic function divides the data into two groups.

Note that the logistic regression did not classify the beef with 100% accuracy as there are two observations that were erroneously classified. Nevertheless, the logistic regression can have multiple predictors, thus using more than one dependent variable may increase the predictive power of the model.

The Maximum Likelihood method mentioned above enables the fitting of models with distributions with different shapes. The models that fit the data with distributions with different shapes, and not only normal distributions (or bell curve shape), are called Generalized Linear Models (GLM). Logistic regression employs the Cumulative Binomial distribution, which has an S-shaped distribution similar to the logistic function. Logistic regression, is thus, a binomial regression model. Logistic regression is not called binomial regression because there are other types of binomial regression. If you are familiar with the statistical software R, the logistic regression can be fitted using the glm() function calling the binomial distribution, as shown below. Because logistic regression is the most popular binomial GLM, no additional code specification is required; for other binomial models, a link function is added.

Model <- glm(y ~ x, family=”binomial”)

In summary, logistic regression is a model that uses an S-shaped curve to divide the data into two groups, a split that is typically performed at the center of the curve. When used with multiple dependent variables, logistic regression becomes a powerful and valuable tool for analyzing and understanding various aspects of animal production and other fields.

Thanks for reading, and I hope you found this post helpful!

Christian Ramirez-Camba