The degrees of freedom give you the freedom to conclude whatever you want

The concept of degrees of freedom is fundamental in statistics, but it can be difficult to grasp. Ignoring its importance can lead to incorrect conclusions in research studies, which can lead to financial losses for livestock producers. The goal of this post is to look at why we use degrees of freedom in statistical tests and why this concept is important to avoid producing inaccurate results that mislead our audience.

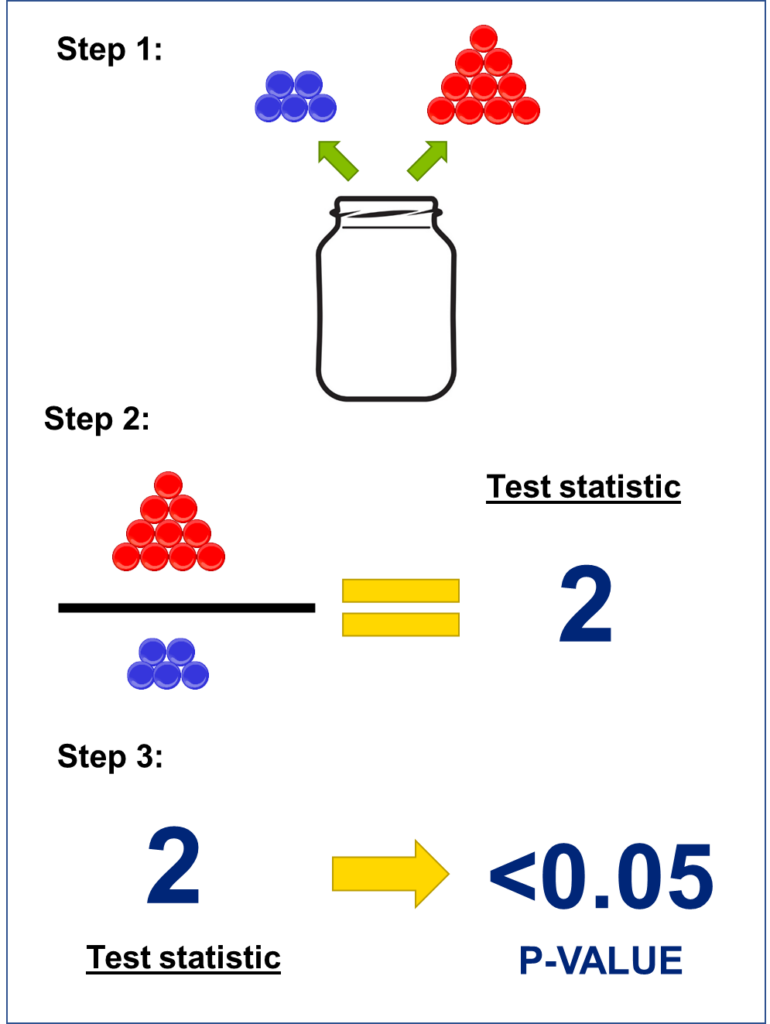
To understand the concept of degrees of freedom, it is necessary to first understand how p-values are calculated. To illustrate p-values, let us use an analogy. Imagine you have a jar containing both red and blue marbles, but you cannot see inside the jar. You wish to determine whether the proportion of red and blue marbles is similar. To do so, you randomly select a total of 15 marbles from the jar. In this scenario, let us assume that you have chosen 10 red marbles and 5 blue marbles. Comparing the two groups of marbles we picked, you obtain a ratio of 2:1 between red and blue marbles. The ratio between measurements in a statistical test is known as the Test Statistic (Figure 1). Over the last few decades, clever statisticians have developed conversion factors between test statistics and p-values. Generally speaking, when the test statistic exceeds 1.8 (known as the critical value), the p-value is less than 0.05. Therefore, a small p-value essentially indicates that two (or more) groups are distinct.

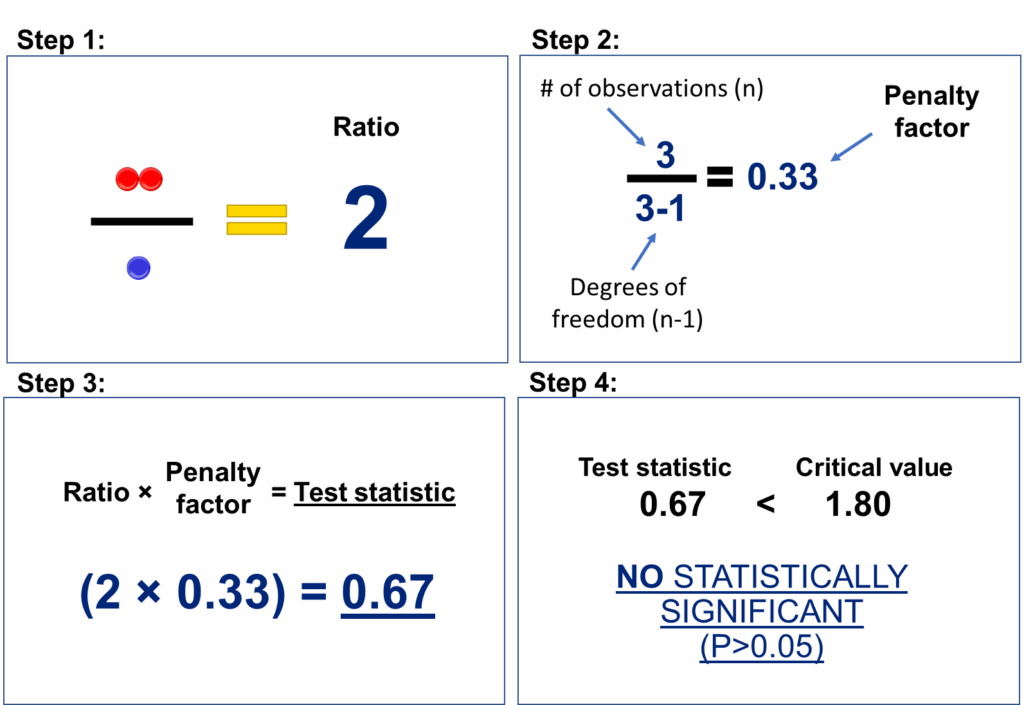
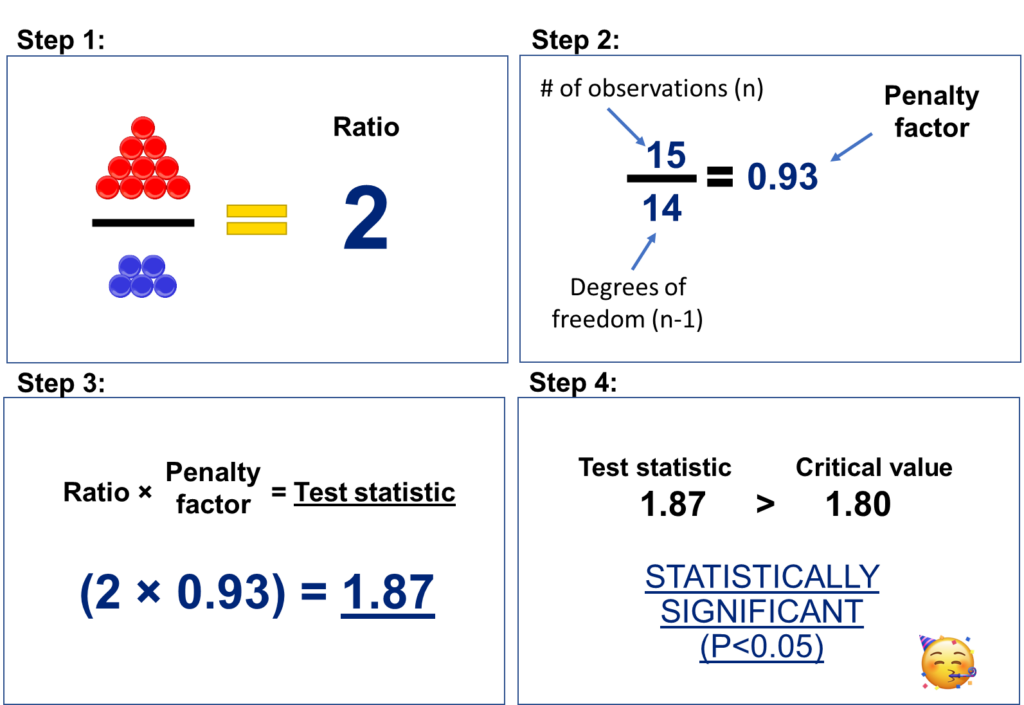
The preceding p-value illustration is incomplete. There is an additional component to the calculation known as the Degrees of Freedom. In terms of applied statistics, it is not necessary to comprehend the specifics of degrees of freedom. It is only crucial to understand why they are employed, which is to ‘penalize’ your calculations when a small sample size is employed. In the preceding example, let’s suppose that instead of selecting 15 marbles, you only pick three, and you get 2 red and 1 blue marble. In this instance, you also obtain a 2:1 ratio, and you may infer that there are more red than blue marbles. However, with only three observations, you may not feel confident about the findings. Hence, the degrees of freedom penalize your experiment for employing only a small sample size. The degrees of freedom is a factor applied to the ratio (in this case, 2:1) and involves a proportion between the number of observations (n) and the number of observations minus one (n-1). This proportion impacts your computations when employing a small sample size, but to a lesser degree when using a large sample. For instance, as illustrated in Figure 2, if you have only 3 observations, the penalty factor is 0.33, and your ratio of 2 becomes 0.67. However, if you use 15 observations as demonstrated in Figure 3, the same ratio of 2 becomes 1.87. In this second hypothetical example, a ratio of 1.87 exceeds our critical value of 1.8, indicating that there are statistically significant differences (or P<0.05).

The impact of degrees of freedom on our calculations varies depending on the sample size. For instance, if our sample size is 6, penalizing the calculations with n-1 has a important effect, resulting in a reduction of the calculated ratio by 17% (5/6 = 0.83). However, if we use a larger sample size, such as 1000 observations, the penalty imposed by n-1 is minimal, with only a 0.1% reduction of the calculated ratio (999/1000).

In both hypothetical experiments conducted with either 3 or 15 marbles, it was observed that there are more red marbles than blue. However, in the experiment with only 3 marbles, the test statistic of 0.67 indicates that statistically significant differences between the marbles were not detected. The lack of differences could indicate either the absence of actual differences or a penalty on our calculations due to the experiment’s small sample size. In essence, our own computations may limit our ability to detect differences, implying that the p-value reflects not only the results of the experiment, but also the method’s bias.

Statistical tests are intentionally designed to penalize small samples based on the principle of “innocent until proven guilty”. In the experiment involving three marbles, although the number of red marbles exceeded the number of blue ones, the evidence is not conclusive. The results of the experiment could be completely altered if a fourth marble were selected and it turned out to be blue. In the absence of conclusive evidence, it is therefore preferable not to discriminate against marbles. As a result, we can conclude in statistical testing that two groups are different (P<0.05) or that we have failed to demonstrate that they are different (P>0.05). We cannot, however, conclude that the two groups are similar.

After determining that there is insufficient evidence against a hypothesis, the next logical step is to gather more evidence. However, it is a frequent practice in animal sciences to conclude that groups performed similarly, as discussed in previous posts. This practice can be problematic, especially when accepting hypotheses based on a low number of observations, as it allows scientists to draw arbitrary conclusions. In the previous experiment with three marbles, for example, researchers could claim that there were no differences between red and blue marbles in the jar because the jar was sprayed with an anti-red marbles solution. A naive entrepreneur might use these findings to launch a company that sells an anti-red marbles solution, unaware that bankruptcy is just around the corner.

Final remarks:

Multiple times I have come across research proposals in which the experiment is designed with a small sample size, yet in the same proposal, it is stated that a statistical method will be employed that penalizes the experiment for using a small sample size. So, in essence, the researcher proposes an experiment that will yield little evidence and a method that will penalize that little evidence. Consequently, the most likely outcome is obtaining a P-value greater than 0.05. The appropriate conclusion in this case must be that there is insufficient evidence to reach a reliable conclusion. Nonetheless, these experiments frequently lead to bold conclusions. Don’t get me wrong: studies with small samples provide valuable information; however, this information must be carefully interpreted.

Question for the reader:

• Why wasting time and money in an experiment that most likely would result in P>0.05?

Thanks for reading, and I hope you found this post helpful!

Christian R

Footnotes:

• The marble analysis was inspired by a two-sample t-test, but it is not a real statistical test. Statistical tests, in general, do not assess differences in the number of observations (marbles), but rather differences in characteristics such as variance (ANOVA) or means (Tukey or t-tests) between groups.